论文笔记 - Learning Discriminative Model Prediction for Tracking

Posted on Edited on In Views:

前言

DiMP是Martin大神的新作，这篇作品不同于CVPR2019中大量使用的SiamRPN系列，而是通过针对Siamse系列对于背景和目标的区分性不足的确定，进行改善。在这篇论文中，作者设计了一种具有判别能力的Loss，并且通过end-to-end的训练学习Loss重点的关键参数。结合权重预测模块，对网络进行良好的初始化，最终DiMP在速度和准确性的都有所提高，在VOT2018数据集上，EAO达到0.440，且FPS达到40.

论文：Learning Discriminative Model Prediction for Tracking

背景

单目标跟踪解决的是任意物体的跟踪问题，与其他计算机视觉任务不同，单目标跟踪的目标信息只能在测试时拿到，因此，要在测试时根据目标的信息对神经网络进行端到端进行训练比较困难。

近年来，Siamese系列比较好的解决了这个问题。即在off-line训练时，通过端到端的训练，让神经网络学习一种feature embedding来表征图片，在跟踪时，通过图片embedding和待搜索区域的embedding进行卷积，计算出相似度，找出最相似的区域，从而完成跟踪。
Siamese系列缺点
但是基于Siamese的跟踪方法也有一定的弊端：

  • 在测试时，仅仅使用了目标的外观特征，没有有效利用背景的外观特征。
  • 对于训练集中不包含的物体，通过训练得到的相似性度量并不完全可靠。
  • Siamese方法的模型更新策略并不够强。

创新点

针对Siamese系列的缺点，作者提出了改进方法。首先，作者使用了模型预测网络，并且通过具有判别能力Loss进行优化，此外，作者还设计了快速迭代方法进行优化。作者通过一下方式进行快速迭代：

  • 在每次梯度下降时，朝向梯度最陡的地方，以计算得到的最优步长进行下降。
  • 设计一个权重预测模块，为模型提供较好的初始化。

作者在NFS、UAV123、OTB100、TrackingNet、LaSOT、GOT10k和VOT2018数据集上进行测试，DiMP都取得了State-of-the-Art的表现，且计算速度约为40FPS

本文提出的方法

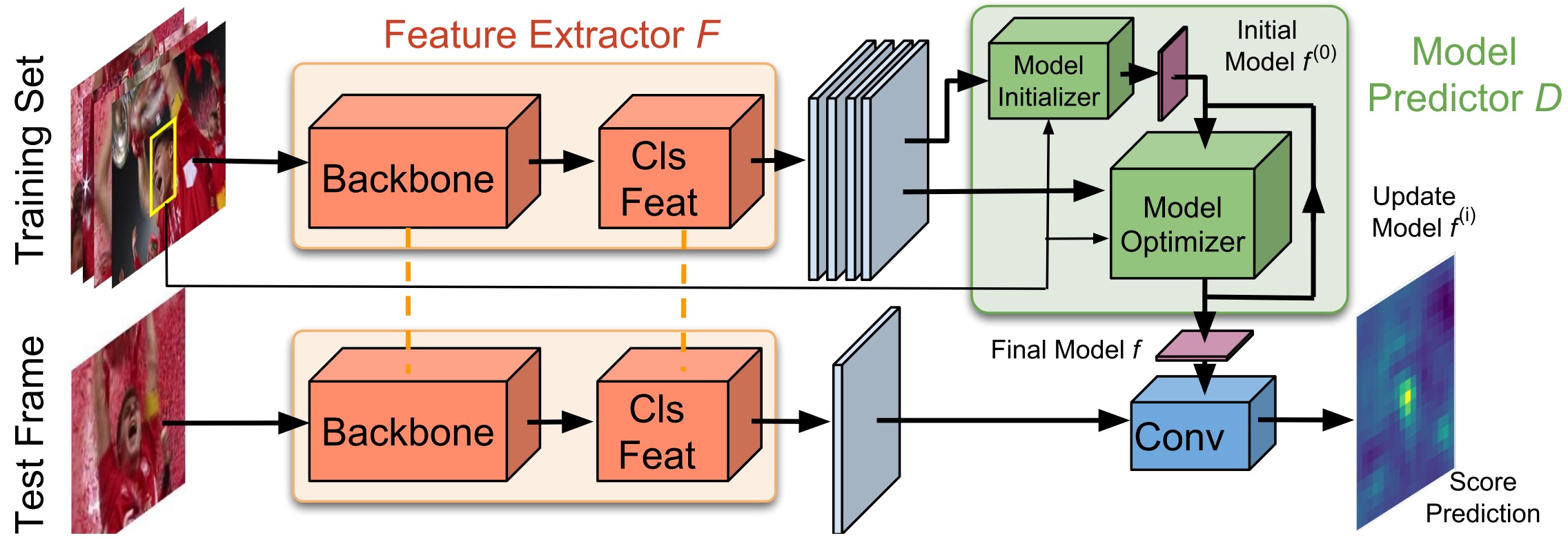Pipeline
作者设计的网络如上图所示，与Siamese系列方法类似，这个网络是可以进行端到端训练的，但与Siamese系列方法不同，该网络可以充分利用背景信息，并且可以通过新数据进行有效的更新。作者依照两个原则进行网络的设计：

  • 能够学习鲁棒模型的具有判别能力的Loss
  • 能够让模型快速收敛的优化策略 遵循这两个原则，该网络可以在快速收敛的同事，保持良好的判别能力。

在进行预测时，模型是由卷积层的权重组成的。这些权重是由Model Predictor根据输入的Bounding boxes和图片帧预测出来的。Model Predictor由以下两部分组成：

  • Initializer: 根据目标的外观特征，提供模型权重的初始估计
  • Optimizer: 根据目标和背景的外观特征，对初始权重进行优化

根据作者的设计，Optimizer只针对少量可学习的参数进行学习，从而避免过拟合，并对未见过的物体保持泛化性。

最终的检测网络由两个branch组成，这两个branch的输入为同一个特征提取网络输出的特征

  • classification branch: 权重由Model Predictor预测得到，区分目标和背景，计算出目标的confidence score
  • bbox estimation branch: 最大化bbox和GT的IOU，对bbox进行refine

上述的两个branch和特征提取网络，都可以通过端对端训练进行优化。

Loss函数

一般来说Loss函数的形式如下所示：

L(f)=1∣S train ∣∑(x,c)∈S train ∣r(x∗f,c)∣2+∣λf∣2L(f)=\frac{1}{ | S_{\text { train }} |} \sum_{(x, c) \in S_{\text { train }}}|r(x * f, c)|^{2}+|\lambda f|^{2}

其中, xjx_j代表feature map，cjc_j为bbox的中心点坐标，S train =(xj,cj)j=1nS_{\text { train }}={(x_{j}, c_{j})}_{j=1}^{n}代表训练集，ff为model的权重，rr代表残差函数，以ss代表x∗fx * f作为heat map。常见的形式为r(s,c)=s−ycr(s,c)=s - y_c，其中ycy_c为以cc为中心的高斯分布。

但是直接使用这种简单的形式搭配MSE进行优化，由于负样例较多，且负样例的label统称为0，这就要求模型足够复杂，来对负样例进行判别，还会导致模型偏向于学习负样例，而不是区分负样例和正样例。

为了解决这样的问题，作者在Loss中加入了权重，并参考SVM中的Hinge Loss，将score map中大量的负样例过滤掉。而对于正样例区域，作者仍旧采用MSE Loss，因此最终的残差函数如下所示：

r(s,c)=vc⋅(mcs+(1−mc)max⁡(0,s)−yc)r(s, c)=v_{c} \cdot\left(m_{c} s+\left(1-m_{c}\right) \max (0, s)-y_{c}\right)

在公示中，下标cc代表对中心点的依赖程度。vcv_c为权重，mc(t)∈[0,1]m_{c}(t) \in[0,1]为Mask，在背景区域，mc≈0m_{c} \approx 0，在物体对应区域mc≈1m_{c} \approx 1，这样就可以在背景区域使用Hinge Loss，在物体区域使用MSE Loss，在这篇论文的设计中，目标Mask mcm_c，spatial weight vcv_c，正则因子λ\lambda，以及回归ycy_c都是可以学习的

优化方法

对于模型ff，一般的优化方法可以用以下方程表示：

f(i+1)=f(i)−α∇L(f(i))f^{(i+1)}=f^{(i)}-\alpha \nabla L\left(f^{(i)}\right)

其中，α\alpha代表步长，∇L\nabla L代表梯度。
但是直接使用这样普通的迭代方法会使得模型的优化速度较慢，这是由于α\alpha与当前模型和数据无关，一直保持恒定导致的。因此需要通过根据梯度下降方向计算最优的步长，首先作者将loss表达成如下形式：

L(f)≈L~(f)=12(f−f(i))TQ(i)(f−f(i))+ (f−f(i))T∇L(f(i))+L(f(i))\begin{aligned} L(f) \approx \tilde{L}(f)= \frac{1}{2}\left(f-f^{(i)}\right)^{\mathrm{T}} Q^{(i)}\left(f-f^{(i)}\right)+\ \left(f-f^{(i)}\right)^{\mathrm{T}} \nabla L\left(f^{(i)}\right)+L\left(f^{(i)}\right) \end{aligned}

其中Q(i)Q^{(i)}代表正定矩阵，此时步长可以根据ddαL~(f(i)−α∇L(f(i)))=0\frac{\mathrm{d}}{\mathrm{d} \alpha} \tilde{L}\left(f^{(i)}-\alpha \nabla L\left(f^{(i)}\right)\right)=0进行求解，得到：

α=∇L(f(i))T∇L(f(i))∇L(f(i))TQ(i)∇L(f(i))\alpha=\frac{\nabla L\left(f^{(i)}\right)^{\mathrm{T}} \nabla L\left(f^{(i)}\right)}{\nabla L\left(f^{(i)}\right)^{\mathrm{T}} Q^{(i)} \nabla L\left(f^{(i)}\right)}

根据Q(i)Q^{(i)}不同，求得的步长也可以得到不同的解释，从而对求解过程进行进一步简化：

  • 假设Q(i)=1βIQ^{(i)}=\frac{1}{\beta} I，可以简化为步长为β\beta的普通SGD
  • 假设Q(i)=∂2L∂f2(f(i))Q^{(i)}=\frac{\partial^{2} L}{\partial f^{2}}\left(f^{(i)}\right)，对于论文中使用的MSE Loss而言，则可以使用Gauss-Newton方法进行优化。

这种优化方法同样也可以用在模型的在线更新上。在在线跟踪时，新的训练样本不停的扩充进训练集中，通过将当前模型作为初始化模型，在新的训练集上进行优化即可。
优化算法

模型初始化

为了减少优化的步数，需要使用Initializer来进行很好的初始化。Initializer由一个卷积层和ROI Pooling层组成，有特征提取模块提取得到的模型经过卷积层和Pooling层后变成统一大小，取平均后，就到的初始化的模型权重。此后，这些权重由Optimizer进行优化

通过Loss进行优化

前面提到，Loss中的参数可以在数据集上进行学习。出于对称性考虑，不同的点相对于中心cc的方向并不重要，而距离相对而言更加重要。因此，需要将参数用距离相关函数ρk\rho_{k}和对应的权重ϕk\phi_{k}进行表征，并通过训练学习权重ϕk\phi_{k}。例如ycy_c可以表示为:

yc(t)=∑k=0N−1ϕkyρk(∣t−c∣)y_{c}(t)=\sum_{k=0}^{N-1} \phi_{k}^{y} \rho_{k}(|t-c|)

而ρk\rho_{k}可以表示为：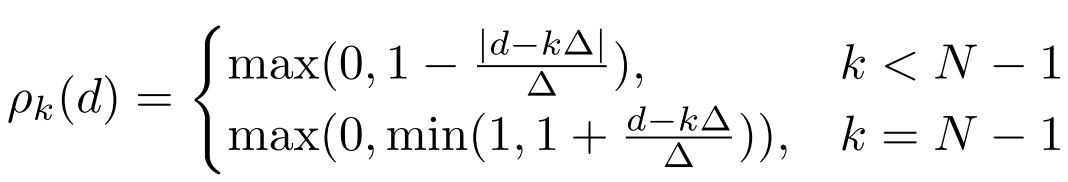

vcv_c和mcm_c也可以进行类似的表征。在实验中，作者取N=10N=10，Δ=0.5\Delta = 0.5。
对于离线训练，用于回归的label ycy_c为高斯分布，vc(t)=1v_{c}(t)=1，mcm_c为tanh函数。而参数ϕk\phi_{k}和λ\lambda为可以学习的参数，最终效果如下所示：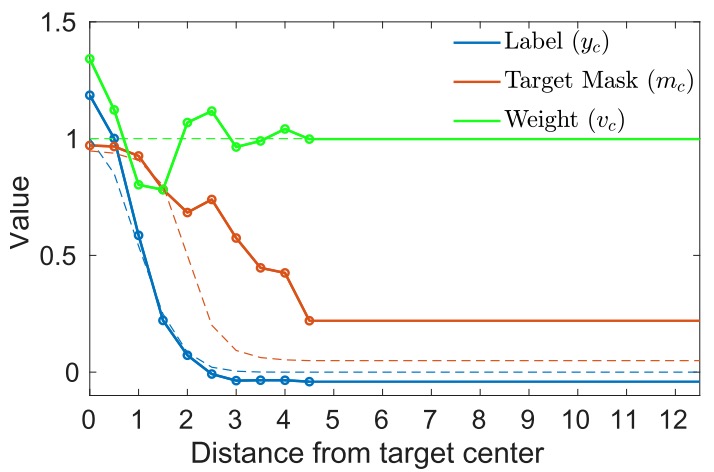
Loss中的参数的GT(虚线)和预测值(实线)

离线训练

作者首先利用视频的前半段和后半段中的部分图片帧构建了训练集和测试集，首先在训练集上根据图片帧和bbox预测模型权重，然后在测试集上进行评估，然后按照下列公式计算误差:

ℓ(s,z)=s−z,z>T max⁡(0,s),z≤T\ell(s, z)=\begin{array}{ll}{s-z,} & {z>T} \ {\max (0, s),} & {z \leq T}\end{array}

然后计算在所有样例上的MSE Loss，在模型优化的每个阶段，都会计算Loss，并进行反传，对模型进行优化(而不是等迭代完成后进行一次BP)。即分类Loss可以表示为:

Lcls=1Niter∑i=0Nincr∑(x,c)∈Stest∣ℓ(x∗f(i),zc)∣2L_{\mathrm{cls}}=\frac{1}{N_{\mathrm{iter}}} \sum_{i=0}^{N_{\mathrm{incr}}} \sum_{(x, c) \in S_{\mathrm{test}}}\left|\ell\left(x * f^{(i)}, z_{c}\right)\right|^{2}

对于IoU branch，作者参考ATOM算法，通过最大化预测的BBox和GT之间的IoU进行优化。

在线跟踪

在进行跟踪时，得到第一帧后，作者使用的Data augmentation构建出包含15帧的初始训练集，使用Initializer预测权重，并通过Optimizer进行10次迭代，得到模型。当跟踪时得到的目标置信度足够高时，训练集会进行扩充，并且每隔20帧迭代2次，或者有干扰物体出现时迭代1次，完成模型的update。

实验

对比实验

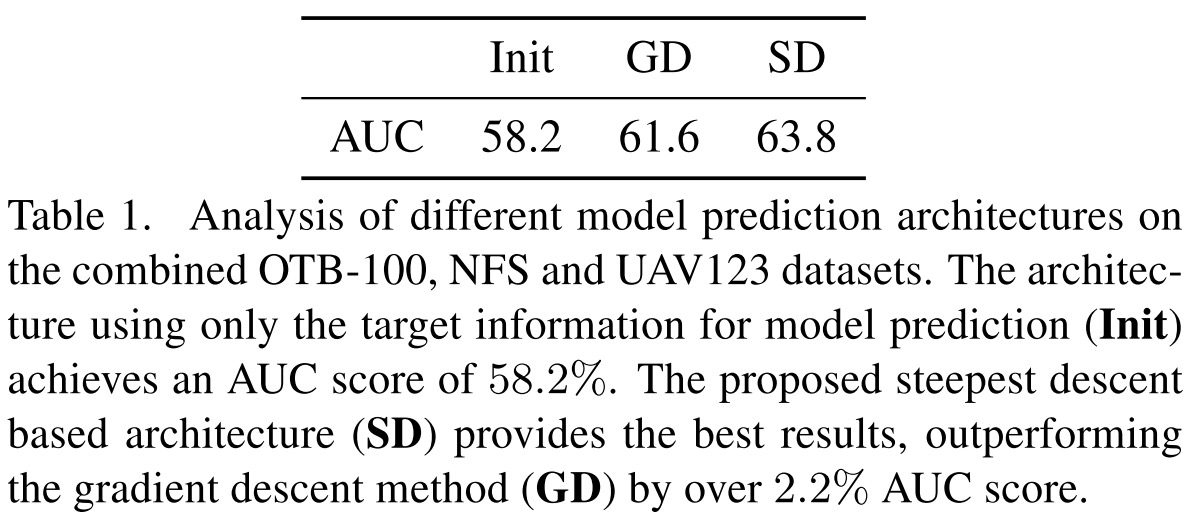只进行Init，使用SGD、本文优化方法的对比不同的创新点对跟踪算法的提升Update算法的影响

  1. 通过只进行Initializer，使用SGD优化，和使用本文方法优化三个实验对比，可以看出优化方法对结果的影响
  2. 通过加入Initializer；放开Feature Extractor的更新；加入卷积层对提取的特征进行卷积，再进行分类；自己学习Loss的参数这几种渐进的改良，可以看出本文创新点都会对跟踪的性能进行提升
  3. 通过不更新、模型取平均、动态更新几种方式的对比，可以看出模型更新策略的重要性。

Benchmark

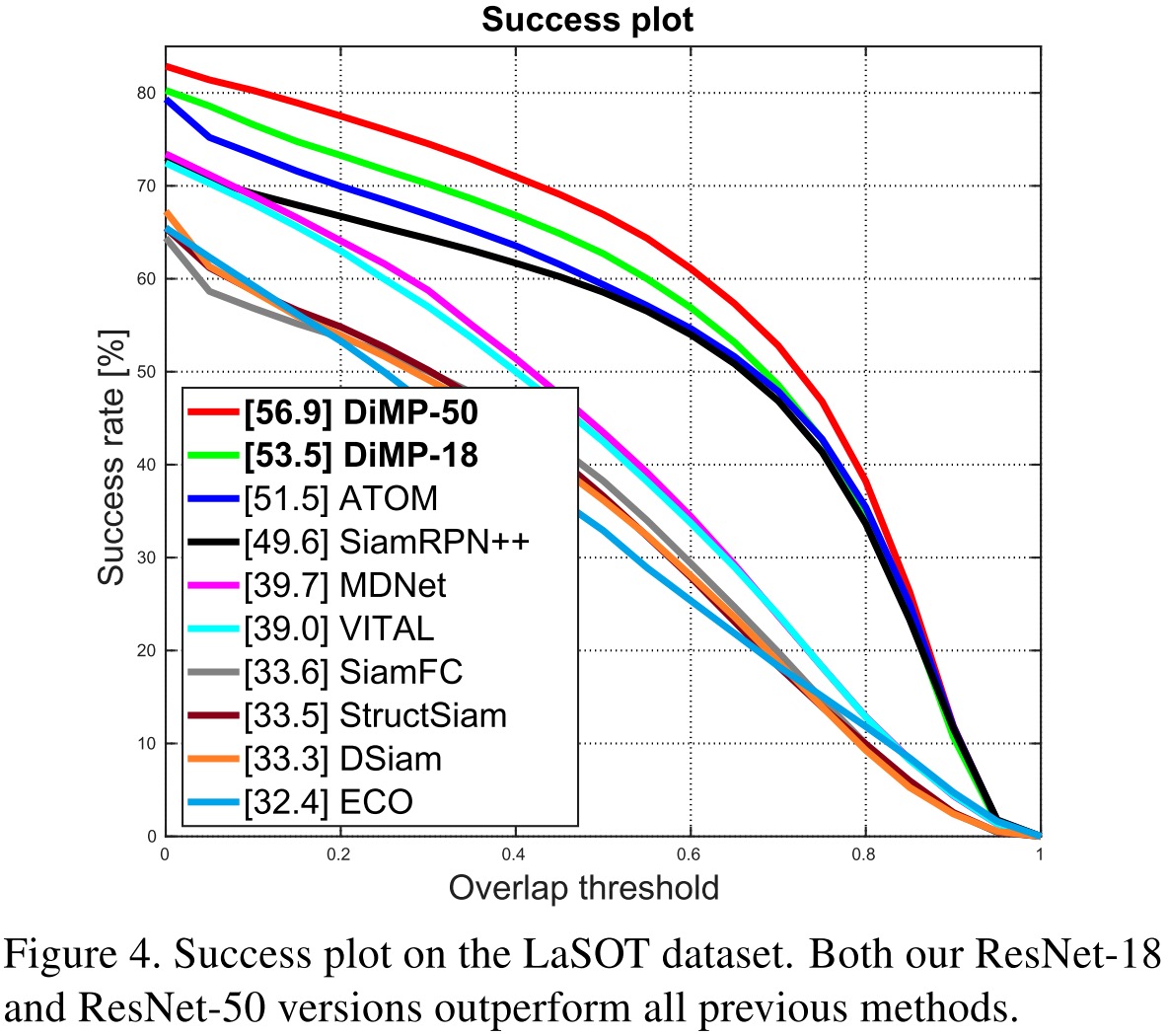
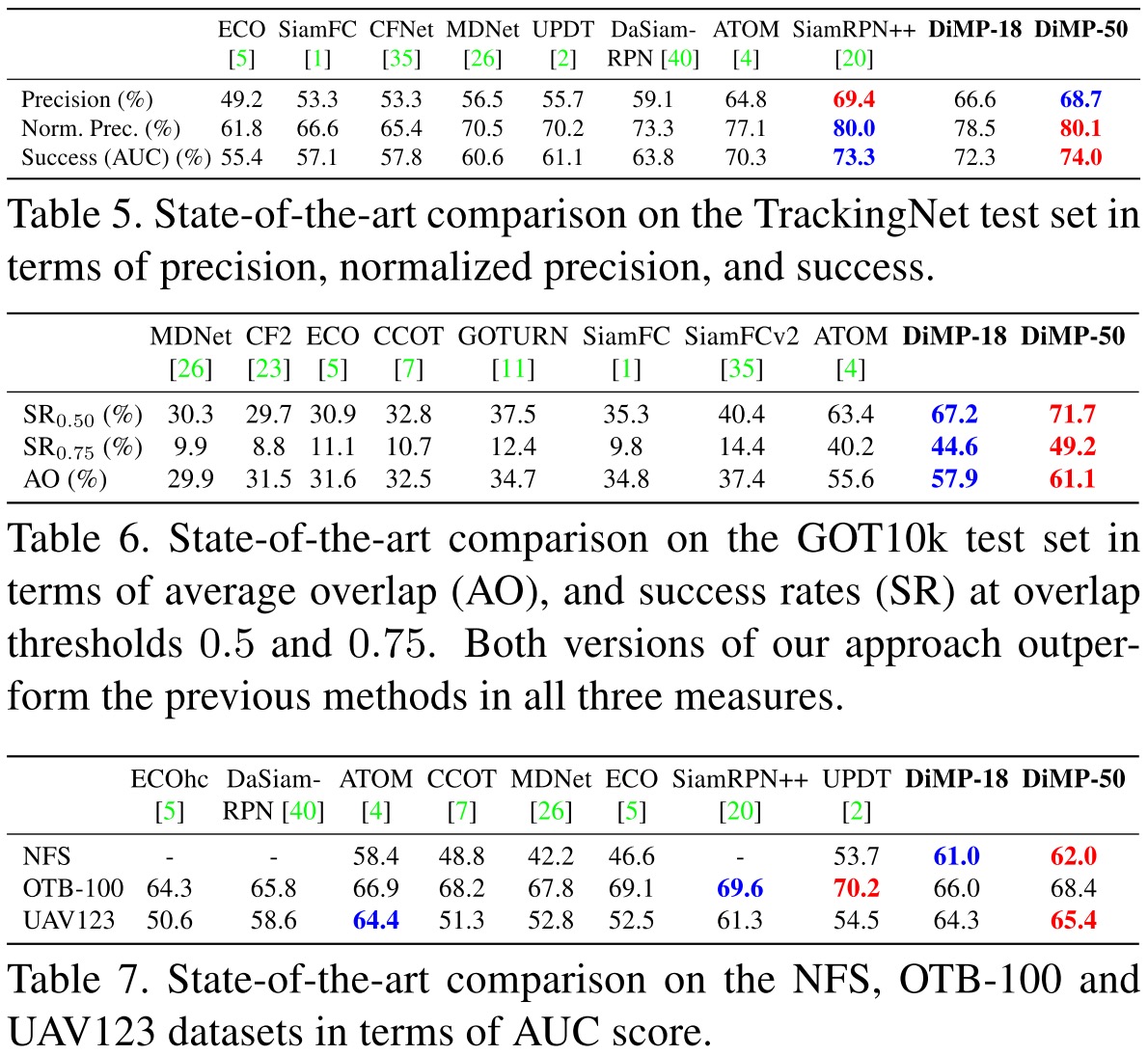
在各大数据集的结果上看，DiMP都取得了State-of-the-Arts的效果。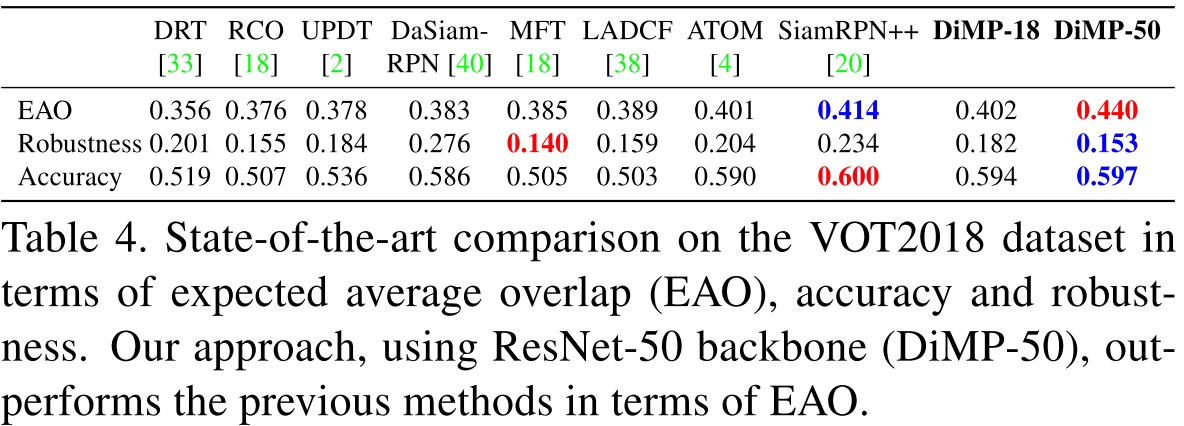

总结

在这片论文中，作者并没有追随最近比较热的SiamRPN系列算法那，而是针对Siamese系列的跟踪方法进行了改良，通过Loss的设计，模型预测和优化的方法，以及对SGD的改进，将单目标跟踪算法的性能继续拔高。

目前代码已经开源，可以学习一下：
代码：DiMP